Online ideal gas, pv=nrt calculator. The oldest and simplest equation of state is the ideal gas law.
Ideal Gas Law Equation
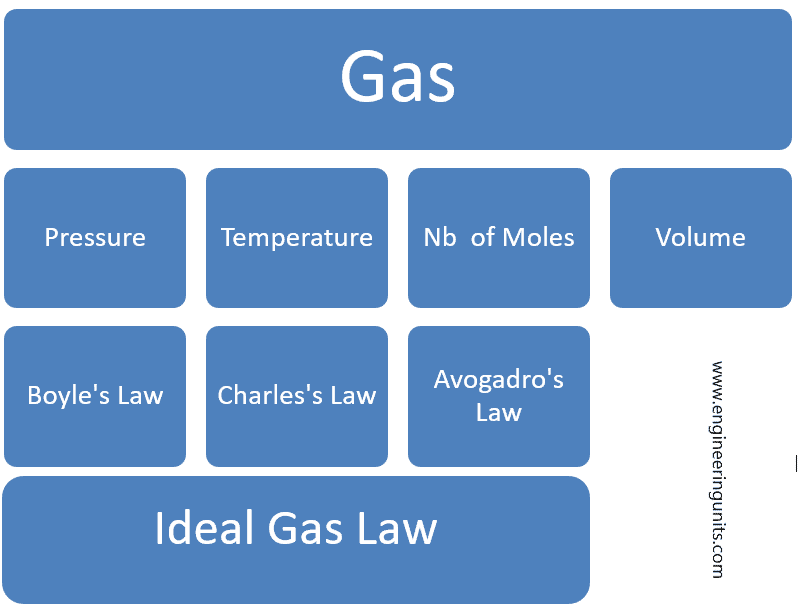
The ideal gas law is an equation of state and comprise the Boyle’s Law, Charles’s Law and Avogadro’s Law into a single statement.
PV = nRT
where:
P = Pressure.
V= Volume.
n= nb of moles of Gas.
T = Temperature.
R = Ideal Gas Constant.
Ideal Gas Law Equation
Assumption Ideal Gas Law
The ideal gas law was stated by Emile Clapeyron which is equation of state relating state variable such as volume, temperature and pressure at given set of physical conditions. The ideal gas law applies only to ideal gas which is define by the below assumption:
- Gas particles are in continuous, rapid, random motion.
- There are no attractive forces between gas particles.
- The gas particles are small compared with the distance separating them.
- Collisions between particles and between particles and the container walls are elastic collisions.
- The temperature of the gas is proportional to the average kinetic energy of the molecules.
In other simple words the ideal gas law applied at low low pressure ( few atmos). and high temperature well above the boiling temperature.
PV=nRT Units
To make sure that we are using the ideal gas law correctly, we should have PV=nRT at the right units.
In SI units, P in pascals, V in cubic metres, n in moles, T in kelvins and R has the value 8.314 J/(K·mol) . if you want to use the PV=nRT in different check the below table or convert to the right unit (or simply use the online ideal gas law calculator on the top).
The unit of pressure times volume are the units of energy, example joules is equal to Pa m3.
| Value R, Gas Constant | units Pressure | Units Volume | Unit Temperature |
| 8.20578 X 10-2 L atm K-1 mol-1 | atm | Litres, L | K |
| 8.31451 X 10-2 L bar K-1 mol-1 | Bar | Litres, L | K |
| 8.314 J K-1 mol-1 | Pa or Nm-2 | cm3 | K |
| 1.987 cal K-1 mol-1 | Pa or Nm-2 | cm3 | K |
PV=nRT Calculator with Steps.
Step 1 :
Ideal Gas Law Formula :
General ideal Gas law formula: PV = nRT .
Different Ideal Gas Law Equations for different unknown (our PV=nRT calculator is based on the below equation):
- Ideal Gas Law for Pressure(P) = nRT / V.
- Ideal Gas Law for Volume(V) = nRT / P.
- Ideal Gas Law for Temperature(T) = PV / nR.
- Ideal Gas Law for Number of Moles of Gas(n) = PV / RT.
- Ideal Gas Law for R=constant= PV/nT
where:
- P = Pressure.
- V = Volume.
- n = Moles of gas.
- T = Temperature.
- R = ideal gas constant.
Step 2 :
State the equation you plan to use and plug in the values.
Examples on Ideal Gas Law Calculator with Steps
Example 1: Ideal gas law solve for moles, pv=nrt solve for n:
Find the number of moles at 300K temperature, 250kPa pressure and 5 liters volume?
Step 1:
Given that:
Pressure(P) = 250 kPa.
Volume (V) = 5L.
Temperature (T) = 300K.
Moles of gas(n) = ?.
Step 2 :
Substitute the specified values in the equation:
Moles of Gas(n) = PV / RT.
n = (250 × 5) / (8.314 × 300) [Since R = 8.314 J K-1 mol-1].
n = 1250 / 2494.2.
n = 0.5011 moles.
Answer :
Number of Moles n = 0.5011 moles.
Use ideal gas law calculator on the top check the bellow results.
R Constant in PV=nRT Calculator.
The gas constant also well-known as the molar, universal, or ideal gas constant, represented by the symbol R. The Gas constant is a physical constant that is introduced in many fundamental equations in the physical sciences, for instance the ideal gas law and the Nernst equation…
Here are some values of R in different units:
| Values of R | Units |
| 8.3144598(48) | kg m2 s−2 K−1 mol−1 |
| 8.3144598(48) | J K−1 mol−1 |
| 8.3144598(48) ×10−3 | kJ K−1 mol−1 |
| 8.3144598(48)×107 | erg K−1 mol−1 |
| 8.3144598(48)×10−3 | amu (km/s)2 K−1 |
| 8.3144598(48) | m3 Pa K−1 mol−1 |
| 8.3144598(48)×106 | cm3 Pa K−1 mol−1 |
| 8.3144598(48) | L kPa K−1 mol−1 |
| 8.3144598(48)×103 | cm3 kPa K−1 mol−1 |
| 8.3144598(48)×10−6 | m3 MPa K−1 mol−1 |
| 8.3144598(48) | cm3 MPa K−1 mol−1 |
| 8.3144598(48)×10−5 | m3 bar K−1 mol−1 |
| 8.3144598(48)×10−2 | L bar K−1 mol−1 |
| 83.144598(48) | cm3 bar K−1 mol−1 |
| 62.363577(36) | L Torr K−1 mol−1 |
| 1.9872036(11)×10−3 | kcal K−1 mol−1 |
| 8.2057338(47)×10−5 | m3 atm K−1 mol−1 |
| 0.082057338 | L atm K−1 mol−1 |
| 82.057338 | cm3 atm K−1 mol−1 |
References: