Biot number (Bi)
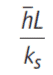
The Biot number, Bi is dimensionless, which is ratio between of the internal and external resistance.
where
- h is the average heat Transfer coeficient.
- L length dimention, The ratio between the volume and the surface area.
- k thermal conductivity.
Drag coefficient (Cf)
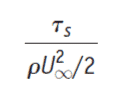
The drag coefficient is the ratio of surface shear stress and the free-stream kinetic energy
Eckert number (Ec)
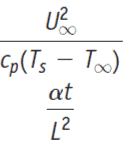
Eckert number (Ec) define he relationship between a flow’s kinetic energy of flow and the boundary layer enthalpy difference. This dimensionless number is used to characterize heat transfer dissipation.
Fourier number (Fo)
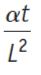
Fourier number (Fo) is a dimensionless number that characterizes transient heat conduction. The Fourier number (Fo) is a time dimensionless number which is the ratio between the rate of heat conduction and the rate of internal energy storage.
Friction factor ( f )
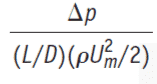
The friction factor f may varies with temperature unknown extent.
The friction factor is dimensionless number is used to estimate the pressure drop for internal flow through ducts or pipe…
Grashof number (GrL)
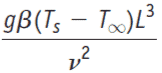
Grashof number, Gr, is the ratio between the buoyant forces and the viscous forces.
Grashof number is dimensionless numbers in heat transfer but specially used also in fluid dynamics.
Colburn j factor ( jH)

j factor is a dimentionless number for heat transfer.The main advantage of the j factor is to determine the heat transfer coefficient, performance prediction of heat exchangers…
Nusselt number (NuL)
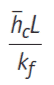
Nusselt number (NuL) is the ratio between the convection heat transfer and conduction heat transfer.
The Nusselt number is correlated with Reynolds number and the Prandtl number
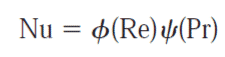
Peclet number (PeL)
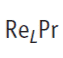
Peclet number (PeL) is the product of Reynolds and the Prandtl number. The Peclet number define the ratio between the advective transport rate and the diffusive transport rate.

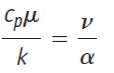
Rayleigh number (Ra)
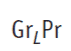
Reynolds number (ReL)
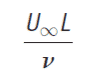
Stanton number (St)
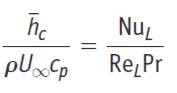
Dimensionless Numbers in Heat Transfer Table

More Heat Transfer Calculator
reference